Nuclear equations are essential tools for understanding radioactive decay and nuclear reactions. They provide a clear representation of how unstable atoms transform into more stable forms by emitting radiation. These equations must be balanced to ensure the conservation of mass and charge‚ following specific rules. For instance‚ in alpha decay‚ an atom emits a helium nucleus‚ reducing its mass number by four and its atomic number by two. Beta decay involves the emission of an electron‚ increasing the atomic number by one while the mass number remains unchanged. Worksheets with answers are widely used to practice balancing these equations‚ helping students master the fundamentals of nuclear physics. By solving such problems‚ learners gain a deeper understanding of radioactive processes and the principles governing them. These resources are invaluable for both educational and reference purposes‚ simplifying complex concepts through structured exercises.

1.1 Importance of Nuclear Equations

Nuclear equations play a pivotal role in understanding the fundamental processes of radioactive decay and nuclear transformations. These equations are not merely theoretical constructs; they have far-reaching practical applications in various fields‚ including medicine‚ energy production‚ environmental science‚ and materials engineering. The importance of nuclear equations lies in their ability to describe the intricate changes that occur within the nucleus of an atom‚ allowing scientists to predict and analyze the outcomes of nuclear reactions.

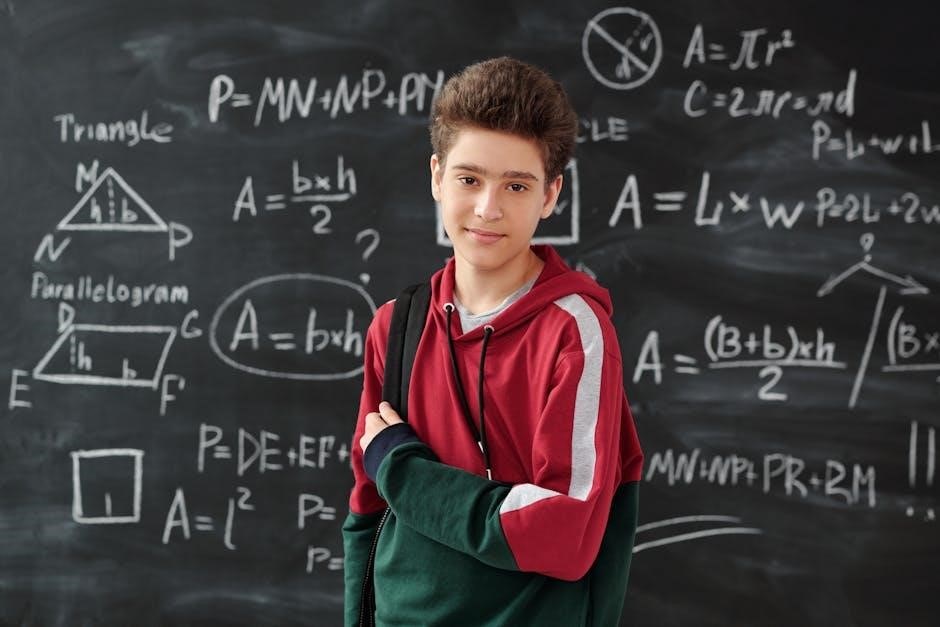
One of the most significant reasons nuclear equations are important is their role in balancing nuclear reactions. The laws of conservation of mass and charge dictate that the total mass number and atomic number on both sides of the equation must be equal. This ensures that nuclear reactions are predictable and follow specific rules‚ such as those governing alpha‚ beta‚ and gamma decay. For example‚ in alpha decay‚ an atom emits a helium nucleus (2 protons and 2 neutrons)‚ reducing its mass number by 4 and its atomic number by 2. Similarly‚ beta decay involves the emission of an electron‚ which increases the atomic number by 1 without changing the mass number. These principles are essential for understanding how unstable isotopes transform into more stable forms.

Nuclear equations are also crucial in the field of nuclear medicine. Radioisotopes are widely used in medical diagnostics and treatments‚ such as cancer therapy. For instance‚ iodine-131 is used to treat thyroid cancer because it emits beta and gamma radiation‚ which can destroy cancerous cells while minimizing damage to healthy tissue. Understanding the nuclear equations involved in the decay of such isotopes allows medical professionals to calculate dosages accurately and ensure safe treatment protocols. Without a grasp of these equations‚ advancements in nuclear medicine would not be possible.

In the energy sector‚ nuclear equations are indispensable for designing and operating nuclear reactors. The process of nuclear fission‚ where heavy nuclei like uranium-235 split into lighter nuclei‚ releases a tremendous amount of energy. This energy is harnessed to generate electricity. By studying the nuclear equations governing fission reactions‚ engineers can optimize reactor performance‚ improve safety‚ and reduce the production of radioactive waste. Additionally‚ the development of fusion energy‚ which involves combining light nuclei to release energy‚ relies heavily on the ability to model and predict nuclear reactions using precise equations.

Environmental monitoring is another area where nuclear equations are vital. Radioactive isotopes are used to track environmental changes‚ such as the movement of water in ecosystems or the dispersal of pollutants in the atmosphere. For example‚ tritium‚ a radioactive isotope of hydrogen‚ is used to study water cycles and groundwater flow. By analyzing the decay patterns of such isotopes through nuclear equations‚ scientists can gather valuable insights into environmental processes and develop strategies to mitigate pollution and climate change.

Furthermore‚ nuclear equations are essential for education and research. Worksheets with answers‚ such as those available in PDF formats‚ provide students with practical exercises to master the balancing of nuclear equations. These resources are particularly useful for learners at the high school and undergraduate levels‚ as they offer a hands-on approach to understanding complex nuclear phenomena. By solving these problems‚ students develop critical thinking skills and a deeper appreciation for the principles of nuclear physics.

1.2 Basic Concepts

Nuclear equations are fundamental to understanding the processes that occur within the nucleus of an atom. These equations represent the transformations that unstable atoms undergo to achieve stability‚ often through radioactive decay. At the heart of nuclear equations are basic concepts that govern how atomic nuclei change‚ including the types of decay‚ the rules for balancing equations‚ and the terminology used to describe these processes.

Radioactive decay is a natural process in which unstable atoms emit radiation to become more stable. There are three primary types of radioactive decay: alpha decay‚ beta decay‚ and gamma decay. In alpha decay‚ an atom emits an alpha particle‚ which consists of two protons and two neutrons‚ effectively reducing its atomic number by 2 and its mass number by 4. For example‚ when uranium-238 undergoes alpha decay‚ it becomes thorium-234. Beta decay involves the emission of a beta particle‚ which is an electron‚ increasing the atomic number by 1 without changing the mass number. Gamma decay‚ on the other hand‚ does not alter the atomic or mass numbers but involves the emission of high-energy photons as the nucleus transitions to a lower energy state.

Understanding these types of decay is crucial for balancing nuclear equations. The rules for balancing these equations are based on the conservation of mass and charge. The total mass number on the left side of the equation must equal the total mass number on the right‚ and the same applies to the atomic numbers. For instance‚ in the alpha decay of uranium-238 to thorium-234‚ the equation is balanced as follows:

238U 92 → 234Th 90 + 4He 2

Here‚ the mass numbers (238 = 234 + 4) and atomic numbers (92 = 90 + 2) are conserved.

Another essential concept is the understanding of key terms in nuclear physics. The atomic number refers to the number of protons in an atom’s nucleus‚ determining the element. The mass number is the sum of protons and neutrons‚ identifying the specific isotope of an element. Radioactive decay involves the transformation of one isotope into another‚ often accompanied by the emission of radiation. Daughter nuclides are the resulting isotopes after decay‚ while parent nuclides are the original unstable isotopes.

Nuclear equations also involve the concept of half-life‚ which is the time it takes for half of a sample of a radioactive substance to decay. This idea is central to understanding the stability and behavior of isotopes. Additionally‚ the decay constant‚ which is the probability of decay per unit time‚ is a key factor in determining the rate of radioactive decay.

Worksheets with answers‚ such as those available in PDF formats‚ provide a practical way to apply these concepts. They offer exercises that require balancing nuclear equations‚ identifying types of decay‚ and calculating half-lives. These resources are particularly useful for students learning nuclear physics‚ as they provide a hands-on approach to mastering the principles of radioactive decay and nuclear transformations.